算法

北航研究生算法作业

homework1

Posted by Stanlei on April 12, 2024

0 参考资料

  • Concrete Mathematics : A Foundation for Computer Science

1 题目

1.1 递推式求解

\[C(n)= \left\{ \begin{aligned} &1 &n=1 \\ &2C(\frac{n}{2})+n–1 &n\ge2 \end{aligned} \right.\]

==请由定理1导出$C(n)$的非递归表达式并指出其渐进复杂性。==

定理1：设$a,c$为非负整数，$b,d,x$为非负常数，并对于某个非负整数$k$，令$n=ck$，则以下递推式 \(f(n)= \left\{ \begin{aligned} &d &n=1 \\ &af(\frac{n}{c})+bn^x &n\ge2 \end{aligned} \right.\) 的解是 \(f(n)= \left\{ \begin{aligned} &bn^x\log_cn+dn^x &a=c^x \\ &(d+\frac{bc^x}{a-c^x})n^{\log a}-(\frac{bc^x}{a-c^x})n^x &a\ne c^x \end{aligned} \right.\)

解：为使得$C(n)$满足$f(n)$形式，令 \(T(n)=C(n)+1= \left\{ \begin{aligned} &2 &n=1 \\ &2C(\frac{n}{2})+n &n\ge2 \end{aligned} \right.\) 由定理1可知，$d=a=c=2,b=x=1$，即$a=c^x=c^1=2$，代入有 \(T(n)=C(n)+1=n\log_2n+2n\) 因此 \(C(n)=n\log_2n+2n-1\) 其渐进复杂性为$\Theta(n\log_2n)$

1.2 $Prim$算法和$Kruskal$算法集成

==由于Prim算法和Kruskal算法设计思路的不同，导致了其对不同问题实例的效率对比关系的不同。请简要论述：==

==1、如何将两种算法集成，以适应问题的不同实例输入？==

==2、你如何评价这一集成的意义？==

解：首先介绍$Prim$算法和$Kruskal$算法，这两个算法是经典的解决连通无向图$G=(V,E)$中最小生成树问题的算法，采取不同的规则选取安全边加入集合中，直至最终生成最小生成树。

$Prim$算法

  • 从任意一个根节点开始构建树集合$A$，每次选取树集合$A$外距离$A$最近的节点加入树集合中，直至得到$G$的最小生成树（覆盖$V$中所有节点）。
  • 时间总代价为$O(V\lg V+E\lg V)=O(E\lg V)$

$Kruskal$​算法

  • 在所有连接森林中两棵不同树的边中，选取最小权值边，直至得到$G$的最小生成树（覆盖$V$​中所有节点）。
  • 先将所有边按权重排序，然后逐个加入不构成环的边，直到生成MST
  • 时间总代价为$O((V+E)\alpha(|V|)+E\lg E)=O(E\lg V)$，这是考虑到$|E|<|V|^2$得到的结论

显然，对于稠密图（具有大量边，而且边的数量接近于顶点数量的平方）或小规模图（顶点数量较少的图）而言（$|E| \sim |V|^2$），$Prim$算法复杂度近似为$O(V\lg V+V^2\lg V)$，$Kruskal$算法复杂度近似为$O(V^2\alpha(|V|)+V^2\lg V^2)=O(3V^2\lg V)$，这是因为$Kruskal$算法需要不停地判断是否构成环路，会遍历大量的无用边；$Prim$算法的复杂度与顶点数量相关，而与边的数量关系不大，更容易找到局部最优解。

而对于稀疏图（边的数量相对于顶点数量较少的图）或大规模图（顶点数量较多、边的数量较少）的情况而言（$|E| \sim |V|$），$Prim$算法复杂度近似为$O(2E\lg E)$，$Kruskal$算法复杂度近似为$O(E\lg E)$，这是因为$Prim$算法在维护最近节点数据结构的过程中，会丢弃大量的无用节点；而$Kruskal$算法是基于边来构建最小生成树的，对于稀疏图中的少量边，$Kruskal$算法更为高效。

因此，对于本题，我们可以得到以下结论：

  1. 集成方法
    • 对于稠密图或小规模图而言，优先考虑$Prim$算法；对于稀疏图或大规模图而言，优先考虑$Kruskal$算法。
    • 此外，对于一些特殊场景，如需要实时更新最小生成树的场景，$Prim$算法由于其局部性质和易于维护的特点，更适合动态变化的情况。
  2. 集成的意义
    • 集成的意义在于面对不同类型的问题实例时能够选择更为高效的算法，在集成后，算法应对不同规模的输入时会呈现比较稳定的时间代价，提高算法的整体效率。然而，二者相差不过是常数级别的时间代价（考虑到$\alpha(|V|)$函数几乎可以视为视为常数），通常情况下执行时间差距不会很大。

1.3 全排列算法分析

==分析以下生成排列算法的正确性和时间效率：==

HeapPermute(n):
//实现生成排列的Heap算法
//输入：一个正整数n和一个全局数组A[1..n]
//输出：A中元素的全排列
	if n = 1
		write A
	else
		for i←1 to n do
			HeapPermute(n-1)
			if n is odd
				swap A[1]and A[n]
			else
				swap A[i]and A[n]

解：这个生成全排列的算法伪代码是正确的，算法生成的排列满足不重不漏的原则。下面证明其正确性，并分析其时间效率：

1、正确性：考虑使用归纳法证明本算法的正确性。

  • $k=1$时，显然$1$是$1$的全排列，算法正确。
  • $k=2$时，算法输出$[1,2]$和$[2,1]$正确，且运行结束后保持$[2,1]$顺序不变。
  • $k=3$时，算法输出$[1, 2, 3]$、$[2,1,3]$、$[3,1,2]$、$[1,3,2]$、$[2,3,1]$、$[3,2,1]$正确，且运行结束后交换$A[1]$、$A[n]$得到$[1,2,3]$，为原排列顺序。
  • 假设$k<n(n>3)$时算法成立，即$HeapPermute(n)$能够正确生成前$k$个元素的全排列，且满足$k$为奇数时，运行结束后数组顺序不变；$k$为偶数时，运行结束后数组向右移动一位。
  • 当$k=n$​时
    • 在$n$为偶数时，由于$HeapPermute(k-1)$生成了前$k-1$个元素的全排列，且$k-1$为奇数，运行结束后元素顺序不变，此时交换$A[i]$和$A[n]$实现前$k-1$个元素的更新。随着$i$从$1$增长到$n$，实现了所有元素都在最后一位呆过的现象，从而$HeapPermute(k)$能够正确生成全排列。
    • 在$n$为奇数时，由于$HeapPermute(k-1)$生成了前$k-1$个元素的全排列，且$k-1$为偶数，运行结束后元素顺序向右移动一位，此时交换$A[1]$和$A[n]$能够将新的元素更新到前$k-1$个中。随着$i$从$1$增长到$n$，实现了所有元素都在最后一位呆过的现象，从而$HeapPermute(k)$​能够正确生成全排列。
  • 从而对于任意$n$，上述算法能够正确生成全排列。

2、时间效率

  • 首先写出时间复杂度$T(n)$的递推关系式

    • \[T(n)= \left\{ \begin{aligned} &1 &n=1\\ &nT(n−1)+n &n≥2 \end{aligned} \right.\]

    • 可得

    • \[\begin{aligned} T(n) &=nT(n−1)+n \\ &=n(n-1)T(n-2)+n(n-1)+n\\ &=n(n−1)(n−2)T(n−3)+n(n−1)(n−2)+n(n−1)+n\\ &…\\ &=n!+n!+...+n(n−1)+n\\ \end{aligned}\]
    • 显然$T(n)=O(n!)$

  • 事实上，显然$T(k)>1$，因此在递推式中可以将多余项$n$合并，近似得到$T(n)=nT(n−1)$

1.4 最小元素位置问题

==对于求n个实数构成的数组中最小元素的位置问题，写出你设计的具有减治思想算法的伪代码，确定其时间效率，并与该问题的蛮力算法相比较。==

解：首先给出蛮力算法如下，显然对应的时间复杂度为$O(n)$。

FindMin_BF():
//输入：一个数组A[1..n]
//输出：A中最小元素的位置
	min = A[1], pos = 1
	for i←1 to n do
		if A[i] < min
			pos = i
	write pos

具有减治思想算法的伪代码如下：

FindMin(k):
//输入：一个全局数组A[1..n]
//输出：A[:k]中最小元素及其位置
	if k = 1
		return A[1], 1
	min, pos = FindMin(k-1)
	if A[k] < min
		min, pos = A[k], pos
	return min, pos

由于每次减治时问题规模减$1$，且执行算法时间为常数，故时间复杂度为$O(n)$，与蛮力算法的时间复杂度相同。

1.5 约瑟夫斯问题

==请给出约瑟夫斯问题的非递推公式$J(n)$，并证明之。其中$n$为最初总人数，$J(n)$为最后幸存者的最初编号。==

解：首先介绍约瑟夫斯问题的定义。

约瑟夫斯问题：在犹太罗马战争期间，他们41名犹太反抗者困在了罗马人包围的洞穴中。这些反抗者宁愿自杀也不愿被活捉，于是决定围成一个圆圈，并沿着圆圈每隔两个人杀死一个人，直到剩下最后两个人为止。但是，约瑟夫和一个未被告发的同谋者不希望无谓地自杀，于是他迅速计算出他和其朋友在这个险恶的圆圈中应该站的位置

为一般化这一问题，我们在此假设每隔$q$个人杀死一个人。

1、q=1时引理

此时对应每隔1人杀死1人，显然有：

  • 偶数情况下：

    • \[J(2n)=2J(n)-1\]
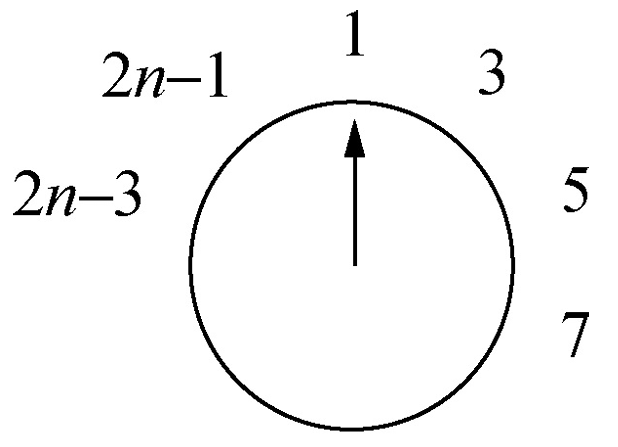
    • image-20240411202803001

  • 奇数情况下：

    • \[J(2n+1)=2J(n)+1\]
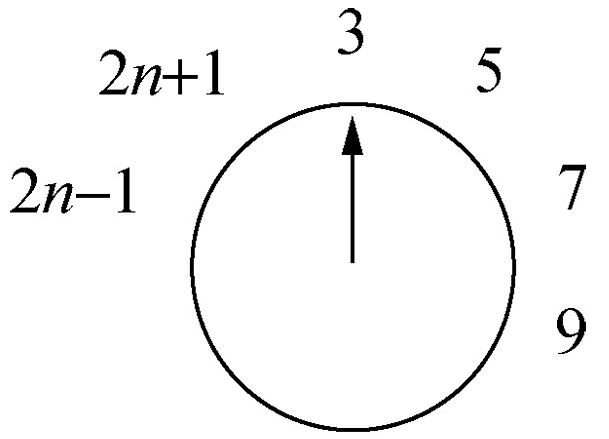
    • image-20240411202934731

  • 因此得到递推表

    • image-20240411203112637

  • 令$n=2^m+l$，其中$2^m$为不超过$n$的最大幂，$l$为余数，则有：

    • \[J(2^m+l)=2l+1,m \ge0,l>0\]

    • 证明：对$m$使用第二数学归纳法

      • $m=0$时，必有$l=0$，此时$J(1)=1$，结论成立
      • 假设$2^m+l<n$时成立，
        • 若$n=2k$，则$J(2^m+l)=2J(2^{m-1}+\frac{l}{2})-1=2(2\frac{l}{2}+1)-1=2l+1$
        • 若$n=2k+1$，则$J(2^m+l)=2J(2^{m-1}+\frac{l-1}{2})+1=2(2\frac{l-1}{2}+1)+1=2l+1$
      • 故$J(2^m+l)=2l+1$对所有的$m\ge0$成立。

  • 因此有

    • \[J(n)=2(n-\lfloor \log_2n\rfloor)+1\]

  • 事实上，$J(n)$有更加简单（直接）的计算公式：

    • 关键在于使用二进制表示$n$
    • $J(n)=2^{v(n)}-1$，其中$v(n)$为$n$的二进制表示中$1$的个数，例如$J(10_{10})=J(1010_2)=2^2-1=3$，在此不再证明，原理是使用移位公式来表示$J(n)$的递推

2、讨论约瑟夫在当年面临的$q=2$​时的问题。

  • 利用类似的方法可以得到

    • \[J_3(n)=\lceil\frac{3}{2}J_3(\lfloor\frac{2}{3}n\rfloor)+a_n \rceil\mod n+1\]
    • 其中$a_n=-2,1,-\frac{1}{2}$分别对应$n\mod3=0,1,2$的情况

  • 这个递归式的难度远超$q=1$的情况，几乎不能继续求解下去了，但是我们可以给出求解的伪代码：

    • N:=3n
while N > n
	do N:=floor((N-n-1)/2)+N-n
J3(n):=N

  • 为简化伪代码中的复杂赋值，我们可以使用另外的方法简化这一计算过程，即令$D=3n+1-N$来替换$N$，伪代码变为：

    • D:=1
while D <= 2n
	do D:=ceil(3D/2)
J3(n):=3n+1-D

3、一般化问题：针对任意$q$的情况

  • 给出伪代码

    • D:=1
while D <= (q-1)n
	do D:=ceil(qD/(q-1))
Jq(n):=qn+1-D

  • 其中，$D$定义为

    • \[\begin{aligned} D_0^{(q)}&=1\\ D_n^{(q)}&=\lceil\frac{q}{q-1}D_{n-1}^{(q)}\rceil,n>0 \end{aligned}\]
CATALOG
    FEATURED TAGS
    LLM PEFT 书生·浦语 算法 Finetune Deploy Agent Eval